交互式特征轨迹外繁殖交叉与映射算法的多晶型背景模型

背景

遗传作图已经被证明是研究复杂性状遗传结构的有力手段，它刻画了潜在的相互作用数量性状位点(qtl)网络。目前的遗传定位统计模型大多建立在qtl的双等位互作基础上，尚不能对异交群体中广泛存在的多等位qtl及其互作进行分析。

结果

在此，我们建立了一个通用框架来建模和定义多等位qtl之间的上位性。基于这一框架，我们推导出了一种统计算法，用于估计和检验异交种全同胞家族不同qtl间的多等位互作。利用该算法对两种杂合子杨树远交的一个生根能力性状的多等位基因上位性分布进行了全基因组扫描。模拟研究结果表明，多等位qtl的位置和效应可以很好地估计，样本和遗传力适中。

结论

开发的模型和算法提供了一种有用的工具，以便更好地表征衍生自森林树的杂合族的复杂性状的复杂性状的遗传控制，从而填补该组重要但不足的物种的遗传映射中发生的差距．

针对回交、双单倍体、ril和F . l .等试验组合，初步建立了QTL定位方法₂，源自近交系[1-3.］．由于自交系的纯合子，可以直接观察到各种标记的所有标记物的孟德尔（CO）分离，可以直接观察到这种十字架中的两个替代等位基因。在实践中，还有一组巨大的经济性和环境重要性 - 交叉口种类，如森林树木，其中传统的QTL映射方法不能适当地使用。对于这些物种，由于长产生间隔和高杂合子，难以或不可能产生自交系[4.尽管实验性杂交品种已经在实际育种项目中得到了商业应用。

对于一个给定的远交系，一些标记可能是杂合的，而另一些标记可能是纯合的。所有标记可以，也可以不，有相同的等位基因系统之间的任何两个远交系用于杂交。同时，对于一对杂合位点，其沿两条同源染色体的等位基因配置(即连锁期)不能从杂交的基因型分离模式中观察到[5.那6.］．遗憾的是，不同标记的一致数量和其已知的联动阶段是对回复或F的统计映射方法的先决条件₂．Grattapaglia和Sederoff [7.]提出了一种所谓的伪测试回流策略，用于两个差异父母之间的受控交叉中的连接映射。该策略对于那些在一个父母和零核中的测试克罗斯标志物的链接分析是强大的，尽管它未能考虑许多用于交叉交叉的交叉标记和显性标记。Maliepaard等。[8.]，通过正确确定标记的连锁阶段，推导出了许多估计不同类型标记间连锁的公式。已建立了一个通用模型，用以同时估计异交群体中任何标记杂交类型的连锁和连锁阶段[9.那10］．斯塔姆(11]编写了强大的软件，利用不同类型的标记整合遗传连锁图谱。

全SIB家族中QTL映射的统计方法尚未得到充分的关注。林等。[12开发了一个模型，该模型考虑了基因组中等位基因数量的不确定性。Wu et al. [13]使用此模型来重新分析杨树的全SIB系列数据[14]，从而发现了传统方法未发现的新的生物量性状qtl。随着对上位性在控制和维持数量变化中的作用的日益认识[15，将Lin等人的模型扩展到qtl的上位性图谱，从而对一个数量性状的遗传结构进行详细和全面的阐述是至关重要的。然而，公认的上位性理论和模型大多基于双等位基因[16[他们的估计和测试是针对来自自交系的血统进行了[17］．到目前为止，还没有模型和算法来描述异交群体中多等位qtl的上位性。

在本文中，我们将扩展双倍超越的理论，以模拟不同QTL之间的超越，每个等位基因都有多个等位基因。然后基于混合模型实现多晶型背景理论的QTL映射统计模型。我们已经衍生了一种封闭的形式，用于估计Mureallelic QTLS在EM框架内的主要和交互式效果。我们的模型允许遗传学家测试个体遗传成分对特质变异的影响。通过模拟研究研究了估计模型，并通过杨树树的QTL映射的示例进行了验证[18］．该算法已经被打包到一个新开发的软件3FunMap中，该软件用于绘制全同胞家族中的qtl [19］．

添加剂 - 优势模型

随机选择两个杂合线作为父母p₁和P.₂为了生产全脂系列，其中QTL如果两条线具有完全不同的等位基因系统，则QTL将形成四种基因型。让我们μ._紫外线为价值QTL基因型遗传等位基因你（u =1,2）来自父母p₁和等位基因V.（V.来自父p的3,4）₂．基于定量遗传理论，这种基因型值可以分配给添加剂和显性效果，如下：

在哪里μ.整体意味着，α._你和β_V.等位基因（添加剂）效果等位基因你和V.分别为,γ._紫外线是QTL的互动（主导）效应。考虑到两个父母之间的所有可能的等位基因和等位基因组合，总共有四种添加剂效应（α.₁和α.₂来自父母的p.₁和β_3.和β_4.来自父母的p.₂和四种主导效应（γ.₁₃那γ.₁₄那γ.₂₃和γ.₃₄）.但这些加性和显性效应不是独立的，因此是不可估量的。参数化后，有两个独立的加性效应，α.=α.₁= -α.₂和β_3.=β_3.= -β_4.，一个主要的影响，γ.=γ.₁₃= -γ.₁₄= -γ.₂₃=γ.₂₄，以估计。

让我们你= (μ._紫外线）_4×1和A.= (μ，α，β，γ）^T.，可以通过设计矩阵连接D.．我们有

在哪里

a的表达式可以由的表达式得到你由

Additive-dominance-epistatic模型

如果在全同胞家族中存在两个分离的QTL，则需要考虑其非等位互作的上位性效应。近亲繁殖家庭的上位论[16可以很容易地扩展到指定远系杂交的不同上位性成分。考虑两个上位性多等位QTL，每个QTL在远交后代中有4个不同的基因型，13、14、23和24。让我们{\mathrm{\mu .}}_{{你}_1{\mathrm{V.}}_1∕{你}_2{\mathrm{V.}}_2}是QTL基因型的基因型值你₁V.₁/你₂V.₂为你₁那你₂= 1,2和V.₁那V.₂= 3,4和你 = （{\mathrm{\mu .}}_{{你}_1{\mathrm{V.}}_1∕{你}_2{\mathrm{V.}}_2}）是相应的均值向量。将2个qtl基因型值划分为以下不同的组分:

在哪里

1. （1）

   μ.总体意思是;

2. （2）

   α.₁为第一个QTL上等位基因1 ~ 2的替换所产生的加性效应;

3. （3）

   β₁为第一个QTL上等位基因3 ~ 4的替换所产生的加性效应;

4. （4）

   γ.₁由于来自不同父母的等位基因之间的相互作用，是主要的效果;

5. （5）

   α.₂为第二个QTL上等位基因1 ~ 2的替换所产生的加性效应;

6. （6）

   β₂是由于等位基因3 ~ 4在第二个QTL上的替换而产生的加性效应;

7. (7）

   γ.₂由于来自不同父母的等位基因之间的相互作用，是主要的效果;

8. (8）

   我_αα是添加剂×添加性认证效果，因为在第一和第二QTLS的等位基因1至2之间的取代之间的相互作用;

9. （9)

   我_αβ是第1个QTL等位基因1 ~ 2与第2个QTL等位基因3 ~ 4的替换相互作用的加性×加性上位性效应;

10. （10）

    我_βα是添加剂×添加性认识效果，因为在第一个QTL在第一个QTL处的等位基因3至4的子排与第二QTL的等位基因1至2之间的亚排之间的相互作用;

11. （11）

    我_αβ为加性×加性上位性效应，这是由于等位基因3 ~ 4在第1和第2个qtl上的取代相互作用;

12. （12）

    j_αγ由于在第一个QTL处的等位基因1至2的取代之间的取代与第二QTL的显性效果之间的取代与第二QTL的显性效果之间的相互作用，是显性×主导官方效果;

13. （13）

    j_βγ是添加剂×显性性认证效果，因为在第一个QTL处的等位基因3至4之间的取代与第二QTL处的显性效果之间的取代之间的相互作用;

14. (14）

    K._γα是主要的×添加性认识效果，因为在第二QTL在第二QTL处的等位基因1至2的取代之间的显性效果与来自等位基因1至2的取代之间的相互作用;

15. （15）

    K._γβ是主要的×添加性认证效果，由于第一个QTL的主效应与第二QTL等等位基因3至4的取代之间的相互作用;

16. （16）

    L._γγ是主要的×主导剖面效果，因为第一和第二QTLS的主效应之间的相互作用。

两个相互作用QTL的遗传效果参数排列A.= (μ,α₁那β₁那γ.₁那α.₂那β₂那γ.₂那我_αα那我_αβ那我_βα那我_ββ那j_αγ那j_βγ那K._γα那K._γβ那L._γγ）^T.．将基因型值载体和基因效应载体联系起来

在设计矩阵

因此，就基因型值载体，遗传效应载体可以表达，如

如果我们有等位基因1 = 3和2 = 4，对于脱近的家庭，方程式1和3.将分别简化为传统的双等位基因加性-显性和双等位基因加性-显性-上位性遗传模型[20.］．

可能性

假设有一个全SIB系列的大小N来自两个交流线。考虑两种相互作用的QTL用于定量特征。让我们你₁V.₁和你₂V.₂分别在QTL 1和2处表示一般基因型，其中你₁和你₂（你₁那你₂= 1,2）是从父p的等位基因₁和V.₁和V.₂（V.₁那V.₂= 3,4）是父母p继承的等位基因₂．特征值的线性模型(y_我）对于个人来说我受两个qtl的影响记为

在哪里{\xi }_{我{你}_1{\mathrm{V.}}_1∕{你}_2{\mathrm{V.}}_2}如果一个特定的基因型，QTL基因型的指示变量是否定义为1你₁V.₁/你₂V.₂是针对个人的我否则是0E._我残差是否正态分布，均值为0，方差为0σ.²．个人的概率我携带QTL基因型你₁V.₁/你₂V.₂可以从其标记基因型推断出，此条件概率表示为{\mathrm{\omega .}}_{{你}_1{\mathrm{V.}}_1∕{你}_2{\mathrm{V.}}_2|我}[20.］．

赋予特征价值的推定QTL的日志可能性（y）和标记信息（m）给出

其中θ是未知参数的向量，该参数包括条件概率表示的QTL位置\left({\mathrm{\omega .}}_{{你}_1{\mathrm{V.}}_1∕{你}_2{\mathrm{V.}}_2|我}\right)， QTL基因型值\left({\mathrm{\mu .}}_{{你}_1{\mathrm{V.}}_1∕{你}_2{\mathrm{V.}}_2}\right)和残差方差（σ.²）.第一个参数，由θ表示_P.，包含在上述模型的混合比例中，而第二两个，由θ表示_问：，是数量遗传参数。正态分布密度\mathrm{F.} {你}_1 {\mathrm{V.}}_1 ∕ {你}_2 {\mathrm{V.}}_2 （y_{我}）也意味着{\mathrm{\mu .}}_{{你}_1{\mathrm{V.}}_1∕{你}_2{\mathrm{V.}}_2}和方差σ.²．

EM算法

提出了标准EM算法来获取未知向量的估计。通过微分方程(6.）关于两组未知参数（θ_P.，θ._问：），我们有

我们定义

哪个可以被认为是一个人的后验概率我有一个QTL基因型你₁V.₁/你₂V.₂．

在e步骤中，根据个体的标记基因型计算QTL基因型的后验概率我由方程(7.）.在M步骤中，通过解决来估计未知参数的最大似然估计（MLES）\frac{\partial }{\partial \mathrm{\theta .}}日志\mathrm{L.}（\mathrm{\theta .}|y那m）=0.．．估计基因型值和残差的封闭形式为

通过为参数提供初始值，迭代E和M步骤，直到估计稳定。稳定值是未知参数的MLE。注意，可以通过处理定位来估计标记间隔内的QTL位置。使用网格搜索，我们可以从染色体上的日志似然比测试统计数据的峰值从QTL位置获得QTL位置的MLE。

参数估计后，可以进行若干假设检验。通过将原假设表述为，可以检验QTL是否存在

减少的可能性（H._0.）和完整的模型（H.₁)，然后估计其对数似然比(LR)

彩光灯和帽子是下面的马尔斯H._0.和H.₁分别。声明QTL存在的临界阈值可以从排列测试凭经验确定[21］．

对不同遗传效应(包括添加剂)的假设检验(α.₁那β₁那α.₂那β₂),占主导地位的(γ.₁那γ.₂）和添加剂×添加剂（我_αα那我_αβ那我_βα那我_ββ），添加剂×主导（j_αγ那j_βγ），主导×添加剂（K._γα那K._γβ)和显性×显性(L._γγ）可以配制的背景效果，其中相应的NULL假设：

在每个零假设下，基因型值应该受到限制

为H._0.：α.₁= 0，

为H._0.：β₁= 0，

为H._0.：α.₂= 0，

为H._0.：β₂= 0，

为H._0.：γ.₁= 0，

为H._0.:γ₂= 0，

为H._0.：我_αα= 0，

为H._0.：我_αβ= 0，

为H._0.：我_βα= 0，

为H._0.：我_ββ= 0，

为H._0.：j_αγ= 0，

为H._0.：j_βγ= 0，

为H._0.：K._γα= 0，

为H._0.：K._γβ= 0,

为H._0.：L._γγ分别= 0。这些约束中的每一个利用如上所述的EM算法实现，这将导致满足方程的基因型值的MLE（11) -(25)。每个试验(11)-(25)的临界阈值可以从模拟研究中确定。

一个有效的例子

我们使用一个真实的森林树的例子来说明我们的多等位基因认知性QTL定位方法在一个远亲群体。材料为种间F₁混合之间的人口Populus deltoides.(P₁),p . euramericana(P₂）.为QTL映射选择了总共86个个体。通过使用74 SSR标记的分离基因型12×34的标记构建遗传键，该标记覆盖全基因组的822.35cm并含有14个连杆基团。测量了每切割（TNR）的根部总数，并显示出在水培养的外来发展阶段的杂交种群的大变化。

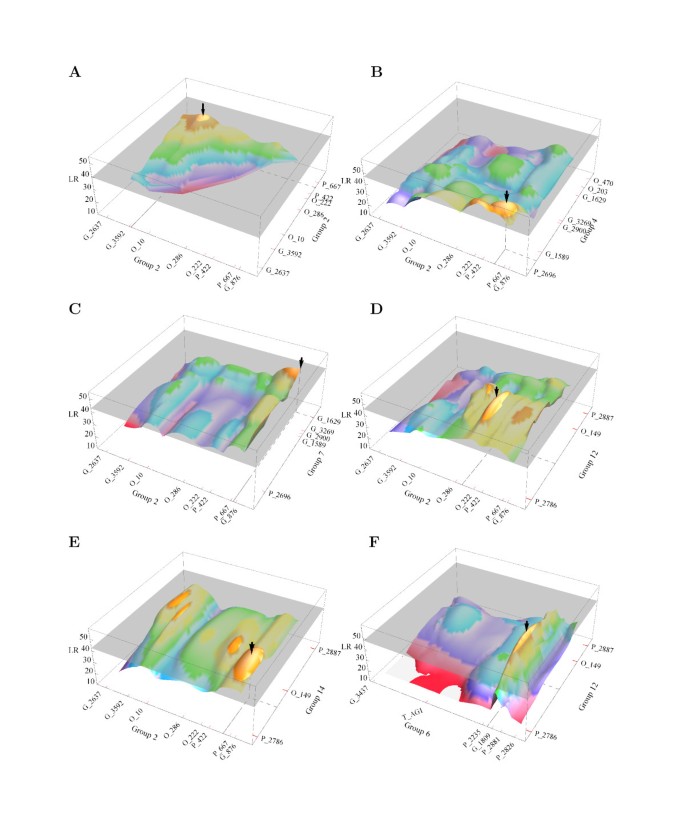
通过对这些连锁群的系统搜索，多等位espistatic模型在5%显著性水平上鉴定了6对来自不同群体的TNR的显著qtl(图1）.通过1000次排列试验确定了断言存在一对相互作用qtl的组×组范围LR阈值。联动组2中存在多个包含qtl的区域，qtl分布在L2_G_3592和L2_O_10、L2_P_422和L2_P_667、L2_P_667和L2_G_876、L2_O_286和L2_O_222标记之间。这些qtl通过相互作用或与4、7、12、14连锁群上的qtl形成5个上位性组合(见表1)1）.第六对来自连接基团6和12。

表格1给出六对相互作用QTL的遗传效果参数的估计。在QTLS on Linkage组2，父母p . euramericana倾向于对根数产生不利等位基因，如许多阴性等位基因所见β值，虽然此父母显示比父级更好的生根容量P. deltoides.．在这些qtl中，亲本P. deltoides.通常为小效果有助于根系，如小α.值。在连锁群6的QTL上，该亲本引发了较大的正加性效应。有趣的是，从总体上看，来自这两个父母的等位基因之间有明显的相互作用γ.价值观，暗示统治生根能力的重要性。在许多情况下，添加剂×添加性认证效果很重要，如许多大的所示我值。我们的模型可以进一步辨别哪种添加剂×添加剂外观贡献。例如，来自连杆组2之间的QTL之间的添加剂×添加剂是由于父母的等位基因之间的相互作用p . euramericana而对于连锁群2和14的QTL对，这是由于来自亲本的等位基因之间的相互作用P. deltoides.．也可以识别QTL如何彼此相互作用的模式×显性，显性×添加剂和显性×显性超越超声（表1）.

蒙特卡罗模拟

我们进行了仿真研究，以研究多晶型外观模型的统计学性质。我们模拟了从两个销售父母的全SIB的样本大小400,800和2000系列。在100厘米长的连杆组的不同位置假设两个QTL，具有6个偶数间隔的标记。模拟每种单独的定量性状的表型值作为这些QTLS加上正常分布的误差的基因型值（扩大为具有不同的遗传性，0.1和0.4）。基因型值以遗传行为和与表格中的真实值的相互作用表示2．

发现QTL位置可以使用我们的模型来估计（表2）.单个qtl的加性效应和加性×加性上位性效应即使在适度的样本量用于适度的遗传力时也可以合理估计。其他遗传效应参数，特别是显性×显性上位性效应，尤其在遗传力较低的情况下，需要较大的样本量才能合理估计。由于涉及的参数很多，异交设计需要比回交或F₂设计。

过去二十年来对开发由着陆器和博特汀（1989年）开创的间隔映射启发的复杂性状的QTL映射的统计模型巨大兴趣[2那3.那17那22-25］．然而，在环境和经济上具有重要意义的物种群体——远交群体中QTL定位模式的建立[26]，没有得到充分的关注。在outcrossing物种中只有几个出版物可用于QTL映射[12那13］．在这篇文章中，我们提出了一个定量遗传模型来研究多等位qtl的上位性，以及一个计算算法来估计和检验上位性互作。

QTL映射的QTL映射的核心问题是如何在不同QTL的多个等位基因之间模拟遗传行为和相互作用。已经开发了传统的定量遗传模型，用于双腿遗传效果[16]他们对多级案例的延伸尚未明确探索。本研究首次尝试尝试表征多级QTL之间的剖面相互作用，该QTL普遍交出群体。我们根据等位基因的不同父母来分区每个QTL的添加剂效应到两个子组件中。同样，我们将添加剂×添加剂简化分为四个不同的子组件，添加剂×显性超越分为两个子组件，以及基于不同父母起源等位基因的相互作用，将显性×添加剂简化分为两个子组件。这些子组件具有独特的生物含义，因为它们来自不同的父母。在实践中，在两个遗传父母父母之间进行杂交，因此了解这些子组分中的每一个有助于研究杂种优势的遗传基础。

我们通过仿真研究测试了新的多级梅雷elic超越模型。通常，由于涉及许多参数，需要更大的样本大小来获得用于在outcrossing群体中的QTL映射的合理精确估计。根据我们的经验，通过精确的表型观察来增加特征的可遗传性可以改善比增强实验尺度的参数估计和模型力量。我们建议对现场管理提供更多的努力，可以提高表型测量质量而不是实验尺寸。通过分析来自杨树遗传学研究的真实数据，新模型得到了很好的验证。有趣的是发现来自不同杨树物种的等位基因之间的相互作用基本上促使来自切屑的能力，大于单独操作的等位基因的遗传效应。这种结果可能有助于了解优势在介质杂种中的作用。

我们建立了一个统计模型来定位异交种全同胞家族的互作qtl。利用传统的数量遗传理论，我们定义了两个异交多等位qtl间相互作用的上位性成分。在此基础上，提出了一种估计异交上位性和检验异交上位性对数量性状控制作用的算法。该模型为研究异交物种(如森林树木)复杂性状的遗传结构提供了一个有用的工具，并填补了这组重要但代表性不足物种的遗传图谱的空白。

国家自然科学基金(NSF/IOS-0923975)、长江学者奖、千人计划等项目资助。

隶属关系

1. 2 .南京林业大学森林遗传与基因工程重点实验室，江苏南京210037

   童春发，张博，徐孟，黄敏仁

2. 美国宾夕法尼亚州立大学统计遗传学中心，宾夕法尼亚州，17033

   Chunfa Tong，钟王＆rongling wu

3. 北京林业大学林业大学林木和观赏植物遗传学和繁殖的国家工程实验室，林业大学遗传学和育种育种中心的计算生物学中心，北京100083

   王忠，庞晓明，司静娜，吴荣玲

通讯作者

对应于鲁格林吴．

作者的贡献

CT对模型进行了推导并进行了计算机仿真和数据分析。BZ和MX收集了杨树杂种的数据。ZW和JS参与了模拟研究。XP参与模型设计和结果解释。MH构想了这个实验。RW开发了模型和算法，协同仿真和数据分析，并撰写了论文。所有作者都已阅读并批准了最终稿。

开放获取本文由BioMed Central Ltd授权发表。这是一篇开放获取的文章，是根据知识共享署名许可协议(https://creativecommons.org/licenses/by/2.0.）提供任何介质中的不受限制使用，分发和再现，所以提供了正确的工作。

再版和权限